energy conservation with spring compression test problems|Chapter 7: Conservation of Mechanical Energy in Spring Problems : exporters A compression spring pushes back when an axial force is applied, allowing engineers to achieve energy conservation in many applications like vibration damping, door locks, and ballpoint pens. Although compression springs appear to have a very simple function, there are multiple factors that engineers must consider when specifying these springs . 11 de mai. de 2023 · Veja um palpite para PSG x Ajaccio, em jogo válido pela 35ª rodada do Campeonato Francês. Na sua última partida, o PSG venceu por 1 x 3 contra o Troyes com gols de Kylian Mbappé ao minuto 8, Vitor Machado Ferreira ao minuto 59, e Fabián ao minuto 86. Na sua última partida, o Ajaccio empatou por 0 x 0 contra o Toulouse.
{plog:ftitle_list}
8 de mar. de 2019 · Como o nome sugere, o Farming Simulator 18 apk mod dinheiro infinito hack para android coloca você no controle de sua própria fazenda, e cabe a .
Chapter 7: Conservation of Mechanical Energy in Spring Problems
flexion compression test
8.8: Sample problems and solutions
We will find the energy of the ball when it is at a height \(h\) above the spring, and the energy of the ball when the spring is fully compressed. . New videos every week! Subscribe to Zak's Lab https://www.youtube.com/channel/UCg31-N4KmgDBaa7YqN7UxUg/Questions or requests? Post your comments .Find the potential energy stored in the spring. A spring operated dart gun fires 10 g darts. Arming the gun requires 185 N of force and results in the shortening of the spring by 10 cm. . (Do not use an equation of motion to solve this problem. Use conservation of energy.) A 68 kg acrobat stands on a spring loaded platform as a part of a stunt.
The spring constant of a spring is 185 N/m. A 0.700 kg stone is attached to the end of the spring. If the maximum velocity of the stone is 5.00 m/s, compute the compression of the spring. A compression spring pushes back when an axial force is applied, allowing engineers to achieve energy conservation in many applications like vibration damping, door locks, and ballpoint pens. Although compression springs appear to have a very simple function, there are multiple factors that engineers must consider when specifying these springs .Assume minimal energy losses due to air resistance, rolling resistance, or other forms of friction and answer the following questions. Determine the speed of the coaster at the top of the loop if the normal force of the rails on the wheels is half the weight of the coaster (that is, if the frame of reference acceleration is ½ g).

From the conservation of mechanical energy (Check our Atom on “Conservation of Mechanical Energy), the work should be equal to the potential energy stored in spring. The displacement x is usually measured from the position of “neutral length” or “relaxed length” – the length of spring corresponding to situation when spring is . Hooke's Law, \(F=-k x\), describes force exerted by a spring being deformed. Here, \(F\) is the restoring force, \(x\) is the displacement from equilibrium or deformation, and \(k\) is a constant related to the difficulty in deforming the system.The minus sign indicates the restoring force is in the direction opposite to the displacement.
foam compression test
8.3 Conservation of Energy; Problems. 8.1 Potential Energy of a System; . What is the elastic spring energy of the cow before the catapult is released? (c) What is the speed of the cow right before it lands on the ground? . Find the compression of the spring in terms of m, M, h, g, and k when the combination comes to rest. (b) The loss of .This problem deals with the conservation of energy in the form of a spring. The formula for the conservation of energy is: We can eliminate initial kinetic energy to get: We have two forms of potential energy in this problem: gravitational and spring. Therefore, we can rewrite the expression to be: There is no initial gravitational potential .potential energy of a spring the stored energy of a spring as a function of its displacement; when Hooke’s law applies, it is given by the expression \(\frac{1}{2}kx^2\) where \(x\) is the distance the spring is compressed or extended and \(k\) is the spring constant conservation of mechanical energy $\begingroup$ Someone in class pointed out that perhaps because the question asks for MAXIMUM compression, they assume gravity does not exist. However, this still doesn't make sense. Assuming gravity does not exist (perhaps it is laid horizontally), the spring would have no elongation.
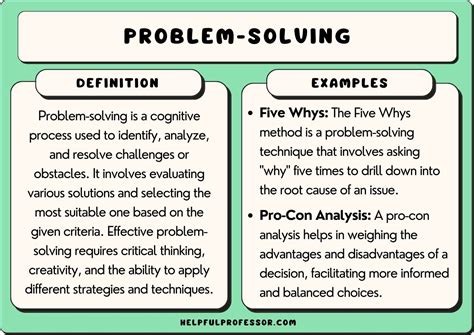
$\begingroup$ For example, if you apply energy conservation at two extremes of the spring i.e, at the maximum compression and maximum extension, you have zero kinetic energy. Therefore, $\Delta U + \Delta KE = 0$ but for our case $\Delta KE= 0$. Which implies, $\Delta U = 0$. This means that at both the opposite extremes, potential energy will be the .Math: Pre-K - 8th grade; Pre-K through grade 2 (Khan Kids) Early math review; 2nd grade; 3rd grade; 4th grade; 5th grade; 6th grade; 7th grade; 8th grade; 3rd grade math (Illustrative Math-aligned)The law of conservation of energy states that the total energy is constant in any process. Energy may change in form or be transferred from one system to another, but the total remains the same. . It will also become apparent that many situations are best understood in terms of energy and that problems are often most easily conceptualized and .
The motion of a mass attached to a spring is an example of a vibrating system. In this Lesson, the motion of a mass on a spring is discussed in detail as we focus on how a variety of quantities change over the course of time. Such .
AP Physics Practice Test: Work, Energy, Conservation of Energy ©2011, Richard White www.crashwhite.com Part II. Free Response m 6. A block of mass m rests on a rough surface, and has a light spring of spring constant k and unstretched length d attached to one side as shown, with the other end of the spring attached to an anchor. There is a
Or in other way, case when spring is just released then it can be thought as, at the mean position it will have potential energy as well as kinetic energy but in the case in which you are bringing the block down the spring slowly It will just have the potential energy.
You can use this problem for self-assessment. Learning Goal: Conservation of Mechanical Energy - spring and roller coaster On the left side of the figure, a 0.11 kg toy car is held to compress a spring. The compression of the spring (from its natural length) is 0.09 m.The spring constant is k = 194.0 N / m.The toy car is released from rest (v 0 = 0), it slides to the .
The mass is attached to a spring with spring constant \(k\) which is attached to a wall on the other end. We introduce a one-dimensional coordinate system to describe the position of the mass, such that the \(x\) axis is co-linear with the motion, the origin is located where the spring is at rest, and the positive direction corresponds to the .If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.For this problem, use Hooke's law: In this formula, is the spring constant, is the compression of the spring, and is the necessary force. We are given the values for the spring constant and the distance of compression. . Use the law of conservation of energy to set these two energies equal to each other: We are trying to solve for .In an ideal spring, the spring force is proportional to its ends’ displacement (x) from the equilibrium position. So, according to Hooke’s Law, F s = -kx. Where F s is the spring force, x is the displacement from the equilibrium position, and k is the spring constant. The spring constant is the characteristic property of the spring.
This problem has been solved! . Question: question 3: Use energy conservation to calculate the maximum compression of the spring from question 2. question 3: Use energy conservation to calculate the maximum compression of the spring .
A science teacher pushes a 0.75 kg cube against an ideal spring with a spring constant of 300 N/m. The spring is compressed to a distance of 5.0 cm. The teacher releases the cube. After moving over the smooth horizontal part of the setup shown in the figure below, the cube slides down over a rough ramp, making an angle of 15° with the horizontal.FACT: Hooke’s Law states that the more a s spring is compressed (or stretched) the more force it applies to restore itself to equilibrium. This is expressed as F s = kx. Q12. A spring with a spring constant (k = 4.0 N/m) is compressed by a force of 1.2 N. What is the total elastic potential energy stored in the compressed spring? (x=0.3 m; U . This is an introduction to how to solve a problem in mechanics using conservation of energy, in the context of a block being pushed up a ramp by a spring. I .
Jogar Derby Crash, um jogo online grátis de carros e 3 dime.
energy conservation with spring compression test problems|Chapter 7: Conservation of Mechanical Energy in Spring Problems